framerate
Barkley's model of an excitable medium

Consider two-variable system of reaction - diffusion equations [1]
∂u/∂t = (1/ε) u(1 - u)(u - uth )
+ Δu ,
∂v/∂t = u - v ,
uth = (v - b)/a .
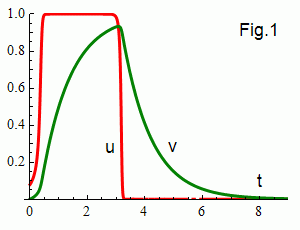
The local dynamics (in the absence of diffusion) is illustrated in Fig.1.
u = v = 0 is the stable fixed point. For u > uth
the variable u (the red curve) switches quickly to 1.
Due to the small parameter ε it is fast in comparison to
the recovery variable v (the green curve) which grows exponentially.
When uth = (v + b)/a exceeds u the excitation is
quenched to 0 and v decays exponentially.
In order to take large time steps a semi-implicit integration scheme is
used [1,2].
On 2D plane the u values are displayed by the red color
and the v values by the green one. Diffusion propagates excitation
through the plane and we get nonlinear waves.
In this script a = 0.5, b = 0.04, ε = 0.02.
As since 8 bit floating point values (in RGBA textures) are not enough,
therefore floating numbers are stored broken in two cells (bytes).
[1] Dwight Barkley
"A model for fast computer simulation of waves in excitable media"
Physica D 49 (1991) 61-70
[2] M.Dowle, R.M.Mantel and D.Barkley
"Fast simulations of waves in three-dimensional excitable media"
Int. Journal of Bifurcation and Chaos, Vol. 7, No. 11 (1997) 2529-2545
Simulations on GPU
updated 14 July 2010

