B-spline basis functions

The equation for k-order B-spline with n+1 control points (P₀ , P₁ , ... , P_n ) is
P(t) = ∑_i=0,n N_i,k(t) P_i , t_k-1 ≤ t ≤ t_n+1 .
In a B-spline each control point is associated with a basis function N_i,k which is given by the recurrence relations (see also b-spline.js)
N_i,k(t) = N_i,k-1(t) (t - t_i)/(t_i+k-1 - t_i) + N_i+1,k-1(t) (t_i+k - t)/(t_i+k - t_i+1) ,
N_i,1 = {1 if t_i ≤ t ≤ t_i+1 , 0 otherwise }
N_i,k is a polynomial of order k (degree k-1) on each interval t_i < t < t_i+1. k must be at least 2 (linear) and can be not more, than n+1 (the number of control points). A knot vector (t₀ , t₁ , ... , t_n+k) must be specified. Across the knots basis functions are C^k-2 continuous.

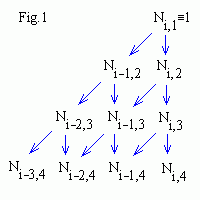
Corresponding iterations scheme for cubic (k = 4) basis functions is shown in Fig.1 . You see, that for a given t value only k basis functions are non zero, therefore B-spline depends on k nearest control points at any point t.

The B-spline basis functions as like as Bezier ones are nonnegative N_i,k ≥ 0 and have "partition of unity" property
∑_i=0,n N_i,k(t) = 1, t_k-1 ≤ t ≤ t_n+1
therefore
0 ≤ N_i,k ≤ 1.
As since N_i,k = 0 for t ≤ t_i or t ≥ t_i+k therefore a control point P_i influences the curve only for t_i < t < t_i+k.

Knot vectors

The shapes of the N_i,k basis functions are determined entirely by the relative spacing between the knots (t₀ , t₁ , ... , t_n+k). Scaling or translating the knot vector has no effect on shapes of basis functions and B-spline. Knot vectors are generally: uniform, open uniform and non-uniform.
Uniform knot vectors are the vectors for which t_i+1 - t_i = const, e.g. [0,1,2,3,4,5].
Open Uniform knot vectors are uniform knot vectors which have k-equal knot values at each end:
t_i = t₀ , i < k
t_i+1 - t_i = const , k-1 ≤ i < n+1
t_i = t_k+n , i ≥ n+1
e.g. [0,0,0,1,2,3,4,4,4] (k=3, n=5).
Non-uniform knot vectors. This is the general case, the only constraint is the standard t_i ≤ t_i+1.

The main properties of B-splines

composed of (n-k+2) Bezier curves of k-order joined C^k-2 continuously at knot values (t₀ , t₁ , ... , t_n+k)
each point affected by k control points
each control point affected k segments
inside convex hull
affine invariance
uniform B-splines don't interpolate deBoor control points (P₀ , P₁ , ... , P_n)

Uniform B-splines

The principle thing to note about the uniform basis functions is that, for a given order k, they are simply shifted copies of one another (because all the knots are equispaced). You can see below, that increasing the order k increases smoothness of a curve and tends to move the curve farther from its control polygon.

Linear B-spline (n = 3, k = 2)

In the right window you see basis polynomials. Move a knot to see how it influences on spline shape and basis functions. B-spline curve is composed of (n-k+2) segments painted in different colors. Corresponding t intervals (in the right window) are painted in the same colors.

Interactive B-spline Use finger or mouse to move a nearest control point (a small blue square in the left window) or knot (a small black square in the right window).

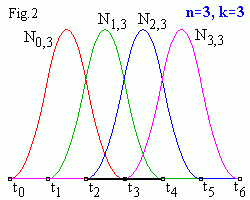
Quadratic B-spline (n = 3, k = 3)

Cubic B-spline (n = 3, k = 4)

Closed curves (n = 5, k = 4)

To make a C^k-2 continuous closed loop you need only, that the last k - 1 control points repeat the first k - 1 ones, i.e. [P₀, P₁, P₂, P₀, P₁, P₂] for n = 5, k = 4 (in this example the last 3 points are displaced a bit to make them visible).

Contents Previous: Building cubic B-spline Next: Nonuniform B-splines
updated 8 August 2001