Periodic points in the Mandelbrot set

A point c in the Mandelbrot set is periodic point with period n if its critical orbit is periodic with period n, i.e. g_n(c) ≡ f_c^on(0) = 0. To the left you see periodic critical orbit with period 3. For example:

g₁(c) = f_c(0) = c = 0
c₁ [1 on the picture below] = 0

g₂(c) = f_c^o2(0) = c² + c = c (c + 1) = 0
c₁ = 0, c₂ [2] = -1

g₃(c) = f_c^o3(0) = (c² + c)² + c = c (c³ + 2c² + c + 1) = 0
c₁ = 0, c₂ [3a] = -1.75488, c₃ [3b] = c₄^* = -0.122561 + 0.744862i

g₄(c) = f_c^o4(0) = 0
c₁ = 0, c₂ = -1, c₃ [4a] = -1.9408, c₄ [4b] = -1.3107,
c₅ [4c] = c₆^* = -0.15652 + 1.03225i, c₇ [4d] = c₈^* = 0.282271 + 0.530061i

The number of such points doubles for each successive value of n because g_n(c) is a polynomial in c of degree 2^(n-1). It is known that it always has 2^(n-1) distinct roots. If c_n is a periodic point, then c_n^* is periodic too. It is evident, that every M-set bulb contains periodic point and corresponding J-set has superstable period-n critical orbit. This point is the nearest to the bulb "center" root of f_c^on(0) = 0 and it can be found e.g. by the Newton algorithm.

Preperiodic (Misiurewicz) points in the Mandelbrot set

A point M_k,n in M is preperiodic with period n if its critical orbit becomes periodic with period n after k (a finite number) steps. It is evident, that preperiodic points M_k,n are roots of equation:
f_c^ok(0) = f_c^o(k+n)(0) or g_k(c) = g_k+n(c) .
We have seen before that for given c the fixed points z₁ = 1/2 ∓ (1/4 - c)^½ (i.e. period-1 orbits) have multipliers λ₁ = 2z₁ = 1 ∓ (1-4c)^½. Therefore any preperiodic point M_k,1 with period 1 has multiplier
λ₁ = 1/2 - (1/4 - M_k,1)^½ .
The plus sign corresponds to the only preperiodic point M_2,1 = -2 (the tip of the Mandelbrot set antenna or the crisis point) with the multiplier λ = 4 . As since multiplier of period-2 orbit is λ₂ = 4(c + 1) therefore multiplier of period-2 Misiurewicz point M_k,2 is
λ₂ = 4(M_k,2 + 1) .
Two examples are M_2,1 = -2 and M_2,2 = i. Its critical orbits are
(0, -2, 2, 2,...) and (0, i, i-1, -i, i-1, -i...)
respectively and their periods are 1 and 2. The orbits are repelling. To see this, the relevant multipliers are
λ₁(-2) = 4 and λ₂(i) = 4(1 + i)
and all of these have absolute value exceeding 1. Preperiodic points are not in a black region of M because there are points arbitrarily close that do not belong to M.
Here are some preperiodic points with period 1. All these points lie outside the main cardioid and the relevant fixed points are repelling.

num	k	c	\|λ\|	Arg(λ)^o
1	2	-2	4	0
2	3	-1.54369	1.67857	180
3	3	-0.22816+1.11514i	3.08738	-23.126
4	4	-1.89291	1.92774	180
5	4	-1.29636+0.44185i	3.52939	-5.7209
6	4	-0.10110+0.95629i	1.32833	119.553
7	4	0.34391+0.70062i	2.45805	-30.988

Real periodic and preperiodic points

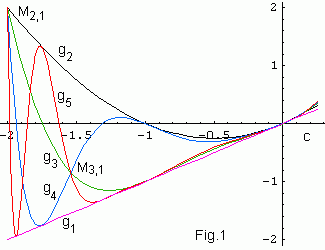For real c real polynomials g_1,2,...,5(c) are shown in Fig.1. Real periodic points are roots of these polynomials. An intersection of two curves g_k(c) = g_k+n(c) corresponds to a M_k,n preperiodic point (M_2,1 and M_3,1 are shown here). Thus Fig.1 let us classify all periodic and preperiodic points in a simple visual way (at least for small n).

Contents Previous: Shaggy midgets Next: Misiurewicz points and the M-set self-similarity
updated 12 Sep 2013