Tangent bifurcations

The left intersection of the green line and parabola is an attracting fixed point because the absolute value of the f(x) slope at the point is smaller than one. The slope at the right intersection is greater than one and it is a repeller. These points meet together at c = 1/4. For c > 1/4 the fixed points become complex and repelling. This is the tangent (or fold) bifurcation.
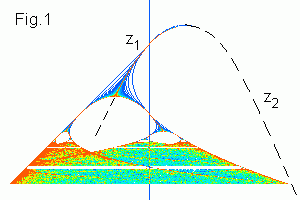
Bifurcation diagram below shows orbits of the critical point zo = 0. You see filaments (and broadening) which show, how iterations converge to the attracting fixed point z1. It is superattracting for c = 0. For c > 1/4 (at the top of the picture) iterations go away to infinity. Repelling fixed point z2 created at the tangent bifurcation is shown in Fig.1.
Tangent

Tangent bifurcation on complex plane

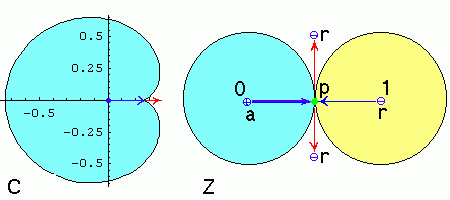Scheme For the quadratic mapping f we have two fixed points
    z1,2 = 1/2 ∓ (1/4 - c)1/2,     λ1,2 = 2z1,2 .
Since z2 = 1/2 - z1 the roots are situated symmetrically with respect to the point p = 1/2. The square root function maps the whole complex plane into a complex half-plane. We choose the Re(z) > 0 half-plane here, therefore the fixed point z2 is always repelling.
While parameter c belongs to the main cardioid on the scheme, the fixed point z1 lies into the blue circle and is attracting and repeller z2 lies into the yellow circle. z1 becomes a repeller too when c lies outside the main cardioid.

For c = 0 we have z1 = 0, λ1 = 0 that is z1 lies in the center of the blue circle and is a superattracting point. z2 lies in the center of the yellow circle. While c goes to 1/4,   z1, 2 move towards the p point. For c = 1/4 the two roots merge together in p and we get one parabolic fixed point with multiplier λ = 1. For c > 1/4, as c leaves the main cardioid, we get two complex repelling fixed points
    z1,2 = 1/2 ∓ i t,   t = (c - 1/4)1/2
where t is real. They go away the p point in the vertical direction.

On the pictures below colors inside filled J sets show how fast a point goes to attractor z1. On the second picture you see infinite sequence of preimages of the attractor, repeller and critical point.
"cauliflower"
When attractor and repeller meet together we get two repellers. There is disconnected Cantor dust below. Blue points go to Infinity now! Repellers with multipliers λ = 1 ∓ 2it generate logarithmic spirals in opposite directions around themselves.

Contents   Previous: Attracting fixed point and period 2 orbit   Next: Birth of Attracting period 2 orbit
updated 12 Sep 2013