Karma model

Two-variable model that capture some essential dynamical features of cardiac tissue was introduced in [1]. This model reproduces an experimentally observed oscillatory 1D pulse instability that causes an alternation in action potential duration. In 2D spontaneous spiral breakup leading to a spatially disorganized electrical wave activity to occur as a direct consequence of this instability.

Temporal dynamics

    dE/dt = F(E, n) = [A - (n/nb)M][1 - tanh(E - 3)]E2/2 - E,
    dn/dt = H(E, n) = ε [Θ(E - 1) - n].
where A = 1.5415. 		 

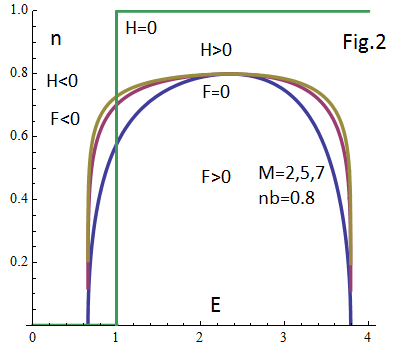
Below you can explore the model for different parameter values. To the left the phase plane of the system is shown. F(E,n) = 0 null cline is the red line and H(E,n) = 0 null cline is the green line. To the right E(t)/4 excitation (black) and n(t) recovery (blue) variables are plotted. The script makes 800 time steps dt.

M nb ε

dt Eo no Ymax field
The system makes an excitation cycle and goes to the stable fixed point (E=0, n=0).

[1] Alain Karma Spiral Breakup in Model Equations of Action Potential Propagation in Cardiac Tissue
Phys.Rev.Lett. 71, 1103 (1993)

Heart rhythms     updated 2 Dec 2011