NonUniform Rational B-splines (NURBS)
Recall, that the B-spline is weighted sum of its control points
P(t) = ∑i=0,n
Ni,k(t) Pi , tk-1 ≤
t ≤ tn+1 (*)
and the weights Ni,k have the "partition of unity" property
∑i=0,n Ni,k(t) = 1 .
As weights Ni,k depend on the knot vector
only, it is useful to add to every control point one more weight
wi which can be set independently
P(t) = ∑i=0,n
wi Ni,k(t) Pi / ∑i=0,n
wi Ni,k(t) . (**)
Then increasing a weight wi makes the point more
influence and attracts the curve to it. The denominator in (**) normalizes
weights, so we will get the equation (*) if we set wi = const
for all i. Full weights wi Ni,k (t) / ∑m=0,n
wm Nm,k(t) satisfy the "partition of unity" condition again.
They are ploted to the right below.
Interactive NURBS
Use finger or mouse to move a nearest control point (a small blue square in
the left window) or change a weight 0 < wi < 5
(a small black square in the right window).
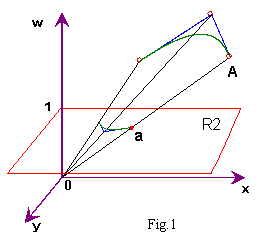
Perspective projection
Formula (**) has a simple interpretation by perspective projection from
4D space (x, y, z, w). The perspective projection from three dimensions
(x, y, w) to two dimensions (the plane
R2) is illustrated in Fig.1. A 3D point A is
projected along a straight line through the origin to the point of intersection
with the plane R2. This is essentially the same process as projecting
a 3D object onto a 2D screen with perspective camera.
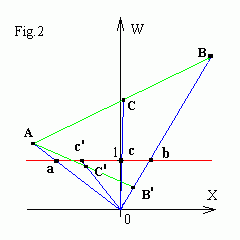
You see in Fig.2, that perspective projection c of a point
C = (A+B)/2 is really attracted to b
with respect to c' projection of C' =
(A+B')/2, for Bw > Aw
and B'w < Aw .
As since perspective projection of a 4D point (x, y, z, w) has
coordinate (x/w, y/w, z/w), therefore formula (**) is the perspective
projection of 4D equation
P w(t) =
∑i=0,n Ni,k(t)
Piw ,
where Piw is a 4D vector with
the components (wi xi , wi yi ,
wi zi , wi ) . The perspective projection
of Piw is evidently the control point
Pi .
4D representation of NURBS is very useful, as since all B-spline's
properties are "projected" into rational spline's ones.
There are two different conventions for representing the control points
in terms of their 4D coordinates (x,y,z,w):
Homogeneous, in which the coordinates represent the point's
position in 4D space. Thus the point's 3D position is (x/w, y/w, z/w).
Weighted Euclidean, in which the coordinates are already considered
to have been divided through. Thus the first tree components (x,y,z)
directly represent the point's position in 3D space and the fourth w
represents its weight.
Weighted Euclidean coordinates are used in interactive
nurbs.js applet.
Conic sections
Conic section is an intersection of a cone with a plane. The angle at which the
plane intersects the cone determines whether the resulting curve is a circle,
ellipse, parabola or hyperbola. Conic curves are represented here using
quadratic NURBS (n=2, k=3) with the open uniform knots [0 0 0 1 1 1]:
parabola (w1 = 1), hyperbola
(w1 = 4) and ellipse (w1 = 1/4).
w1 = 1
w1 = 4
w1 = 1/4
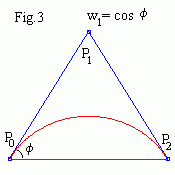
Circular arcs
|
The following method can be used to construct a circular arc of quadratic NURBS:
- The legs of the control triangle are of equal length (i.e. it is isosceles).
- The chord connecting the first and the last control points meets each leg at
an angle φ equal to half the angular extent
of the arc.
- The weight of the inner control point is cos(φ ).
- The open uniform knot vector is [0,0,0,1,1,1].
|
You see below how to get a hole circle with only one NURBS. The knot vectors
are [0, 0, 0, 1/3, 1/3, 2/3, 2/3, 1, 1, 1] and [0, 0, 0, 1/4, 1/4,
1/2, 1/2, 3/4, 3/4, 1, 1, 1].
Contents
Previous: Interpolating cubic B-splines
Next: Tensor product spline surfaces
updated 23 August 2001


