Tusscher-Noble-Noble-Panfilov (TNNP) model

Membrane currents
    I_ion = I_Na + I_K1 + I_to + I_Kr + I_Ks + I_CaL + I_NaCa + I_NaK + I_pCa + I_pK + I_bCa + I_bNa
where I_Na is fast Na⁺ current, I_CaL is L-type Ca ²⁺ current, I_to is transient outward current, I_Kr is rapid delayed rectifier current, I_Ks is slow delayed rectifier current, I_K1 is inward rectifier K⁺ current, I_NaCa is Na⁺/ Ca ²⁺ exchanger current, I_NaK is Na⁺/ K⁺ pump current, I_pCa and I_pK are plateau Ca ²⁺ and K⁺ currents, and I_bCa and I_bK are background Ca ²⁺ and K⁺ currents.

Reversal Potentials
    E_x = (RT/zF) log(X_o / X_i )     for X = Na⁺, K⁺, Ca ²⁺
    E_Ks = (RT/F) log[(K_o + p_KNa Na_o ) / (K_i + p_KNa Na_i )]

Fast Na⁺ current I_Na. The three gates formulation first introduced by Beeler and Reuter is used
    I_Na = G_Na m³h j(V - E_Na )
where m is an activation gate, h is a fast inactivation gate, and j is a slow inactivation gate. Each of these gates is governed by Hodgkin-Huxley-type equations for gating variables and characterized by a steady-state value (m_∞ , j_∞ , h_∞ ) and a time constant for reaching this steady-state value (τ_m , τ_j , τ_h ), which are functions of membrane potential V.
m_∞ (V), h_∞ (V) ≡ j_∞(V) and   7τ_m (V), τ_h (V)/50, τ_j (V)/400 (ms)

are ploted for -100 ≤ V ≤ 50 (mV) (here 0 ≤ y ≤ 1 ). Note, that τ_m (-85) = 0.0011 ms is very small, therefore we have to use Rush and Larsen integration scheme for temporal dynamics simulations. τ_h (20) = 0.18 and τ_j (20) = 0.54 ms.

L-type Ca ²⁺ current I_CaL [2]
    I_CaL = G_CaL d f f₂ f_CaSS 4 ((V - 15)F²/RT) (0.25 Ca_SS e^{2(V - 15)F/RT} - Ca_o ) / (e^{2(V - 15)F/RT} - 1),
    f_CaSS∞ = 0.4 + 0.6/(1 + (CaSS/0.05)²),   τ_CaSS = 2 + 80/(1 + (CaSS/0.05)²),
where d is a voltage-dependent activation gate, f is a slow voltage inactivation gate, f₂ is a fast voltage inactivation gate, f_CaSS is an intracellular calcium-dependent inactivation gate.
d_∞ , f_∞, f_{2 ∞} and   τ_d /2, τ_f /1500, τ_f2 /600.

Transient outward current I_to
    I_to = G_to r s (V - E_K )
where r is a voltage-dependent activation gate and s is a voltagedependent inactivation gate.
r_∞ , s_∞ (mid) and   τ_r /12, τ_s /100.

Slow delayed rectifier current I_Ks [2]
    I_Ks = G_Ks x_s² (V - E_Ks )
where x_s is an activation gate and E_Ks is a reversal potential determined by a large permeability to potassium and a small permeability to sodium ions.

Inward rectifier K⁺ current I_K1
    I_K1 = G_K1 (K_o / 5.4)^1/2x_{K1 ∞} (V - E_K )
where x_{K1 ∞} is a time-independent inward rectification factor that is a function of voltage V - E_K .

Rapid delayed rectifier current I_Kr
    I_Kr = G_Kr (K_o /5.4)^1/2 x_r1 x_r2 (V - E_K )
where x_r1 is an activation gate and x_r2 is an inactivation gate.
x_{r1 ∞} , x_{r2 ∞}, x_{s ∞}, x_{K1 ∞} and   τ_xr1 /1250, τ_xr2 /3.5, τ_xs /1200.

Na⁺/ Ca ²⁺ exchanger current I_NaCa
    I_NaCa = k_NaCa (e ^{γ VF/RT}Na_i³ Ca_o - e ^{(1 - γ) VF/RT}Na_o³ Ca_i α) /
      [(K_mNai³ + Na_o³ ) (K_mCa + Ca_o ) (1 + k_sat e ^{(1 - γ) VF/RT})].

Na⁺/ K⁺ pump current I_NaK
    I_NaK = R_NaK K_oNa_i / [(K_o + K_mK )(Na_i + K_mNa )(1 + 0.1245 e^-11VF/RT + 0.0353 e^-VF/RT)].

Intracellular ion dynamics

The changes in the intracellular sodium Na_i and potassium K_i concentrations are governed by the following equations
    dNa_i /dt = -(I_Na + I_bNa + 3I_NaK + 3I_NaCa ) / V_c F
    dK_i /dt = -(I_K1 + I_to + I_Kr + I_Ks - 2I_NaK + I_pK + I_stim - I_ax ) /V_c F.

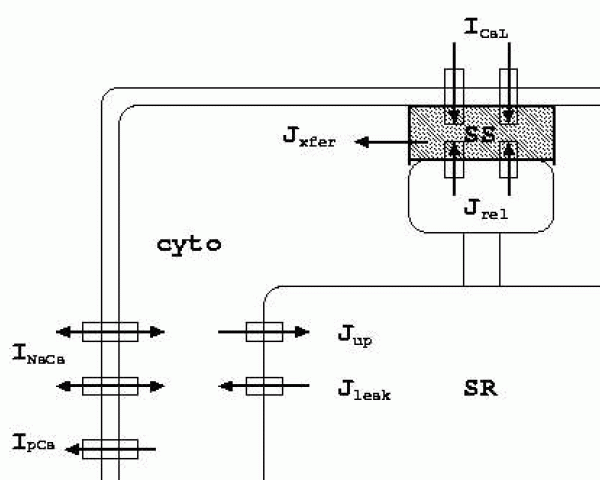
The model contains a description of calcium dynamics in the subspace Ca_SS , cytoplasm Ca_i and sarcoplasmic reticulum Ca_SR
    J_leak = V_leak (Ca_SR - Ca_i ),
    J_up = V_{max up} /(1 + K_up²/Ca_i²)
    J_rel = V_rel O (Ca_SR - Ca_SS )
    J_xfer = V_xfer (Ca_SS - Ca_i )
    O = k₁ Ca_SS² R / (k₃ + k₁ Ca_SS²),
    dR/dt = -k₂ Ca_SS R + k₄ (1 - R),     k₁ = k_1'/k_casr ,     k₂ = k_2' k_casr ,
    Ca_{i buf c} = (Ca_i Bufc) / (Ca_i + Kbufc)
    dCa_{i total} / dt = - (I_bCa + I_pCa - 2 I_NaCa )/2V_cF + (J_leak - J_up ) V_sr /V_c + J_xfer
    Ca_{sr buf sr} = (Ca_sr Bu fsr) / (Ca_sr + Kbufsr)
    dCa_SRtotal /dt = (J_up - J_leak - J_rel )
    Ca_SSbufSS = (Ca_ss Bufss) / (Ca_ss + Kbufss)
    dCa_SStotal /dt = - I_CaL /2V_ss F + J_rel V_sr / V_ss - J_xfer V_c / V_ss
where J_leak is a leakage current from the sarcoplasmic reticulum to the cytoplasm, J_up is a pump current taking up calcium in the SR, J_rel is the calcium-induced calcium release (CICR) current, Ca_itotal is the total calcium in the cytoplasm, it consists of Ca_ibufc, the buffered calcium in the cytoplasm, and Ca_i, the free calcium in the cytoplasm. Similarly, Ca_SR is the total calcium in the SR, it consists of Ca_srbufsr, the buffered calcium in the SR, and Ca_SR, the free calcium in the SR.

The TNNP model scripts are based on Kirsten H.W.J. ten Tusscher's kirstennew2d.f codes (AJP 2006).

[1] Ten Tusscher K.H.W.J., D. Noble, P.J. Noble, and A.V. Panfilov.   A model for human ventricular tissue.   Am J Physiol Heart Circ Physiol 286 H1573 (2004).
[2] Ten Tusscher K.H., Panfilov A.V.   Alternans and spiral breakup in a human ventricular tissue model.   Am.J.Physiol., 90 326-345 (2006).