delay framerate:fps
Use your fingers or mouse to control the model (hold shift key or use mouse wheel to zoom it). Canvas is matched to your browser window.
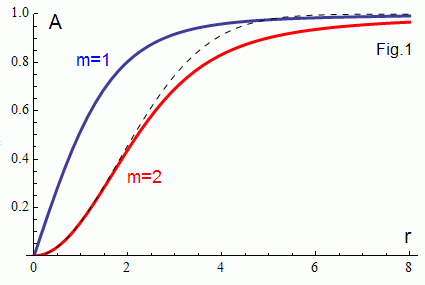
You see m=2 vertex decay into two m=1 vorteces (in a while :) Colors correspond to the vortex phase.

Vortex dynamics

Nonlinear wave equation
∂_t²Ψ = ΔΨ + (1 - |Ψ|²)Ψ
with complex (two components) Ψ(x,y) = u + i v is simulated. Simple explicit scheme is used again (see flat wave) in the fragment shader below

<script id="shader-fs" type="x-shader/x-fragment"> 
precision highp float;
  uniform sampler2D samp;
  uniform sampler2D samp1;
  uniform float dth2;
  uniform float dt2;
  varying vec2 vTexCoord;
  const float d = 1./512.;
void main(void) {
   float u1 = texture2D(samp1, vTexCoord).x;
   float v1 = texture2D(samp1, vTexCoord).y;
   float t = (1 - u1*u1 - v1*v1)*dt2;
   float u =
     2.*u1 - texture2D(samp, vTexCoord).x +
     (texture2D(samp1, vec2(vTexCoord.x, vTexCoord.y + d) ).x +
      texture2D(samp1, vec2(vTexCoord.x, vTexCoord.y - d) ).x +
      texture2D(samp1, vec2(vTexCoord.x + d, vTexCoord.y) ).x +
      texture2D(samp1, vec2(vTexCoord.x - d, vTexCoord.y) ).x +
      - 4.*u1)*dth2 + t*u1;
   float v =
     2.*v1 - texture2D(samp, vTexCoord).y +
     (texture2D(samp1, vec2(vTexCoord.x, vTexCoord.y + d) ).y +
      texture2D(samp1, vec2(vTexCoord.x, vTexCoord.y - d) ).y +
      texture2D(samp1, vec2(vTexCoord.x + d, vTexCoord.y) ).y +
      texture2D(samp1, vec2(vTexCoord.x - d, vTexCoord.y) ).y +
      - 4.*v1)*dth2 + t*v1;
   gl_FragColor = vec4(u, v, sqrt(u*u+v*v), 0. );
}
</script>

Note that u, v, |Ψ| are stored in a float RGBA texture. In this vertex shader |Ψ(x,y)| is plotted. Colors correspond to the phase Arg(Ψ) = atan(v, u).

<script id="shader-vs-show" type="x-shader/x-vertex"> 
  attribute vec2 aPos;
  uniform mat4 mvMatrix;
  uniform mat4 prMatrix;
  uniform float d;
  varying vec3 color;
  uniform sampler2D samp;
  const vec4 dirDif = vec4(0., 0., 1., 0.);
  const vec4 dirHalf = vec4(-.4034, .259, .8776, 0.);
void main(void) {
   float h = .5*texture2D(samp, aPos ).z;
   gl_Position = prMatrix * mvMatrix * vec4(aPos, h, 1.);
   vec3 aNorm = vec3(texture2D(samp, vec2(aPos.x + d, aPos.y)).z -
     texture2D(samp, vec2(aPos.x - d, aPos.y)).z,
     texture2D(samp, vec2(aPos.x, aPos.y + d)).z -
     texture2D(samp, vec2(aPos.x, aPos.y - d)).z, -4.*d);
   aNorm = normalize(aNorm);
   vec4 rotNorm = mvMatrix * vec4(aNorm, .0);
   float i = max( 0., abs(dot(rotNorm, dirDif)) );
   float a = atan(texture2D(samp, aPos).y, texture2D(samp, aPos).x)*.955 + 3.;
   color = vec3( clamp(abs(a - 3.) - 1., 0., 1.),
     clamp(2. - abs(a - 2.), 0., 1.), clamp(2. - abs(a - 4.), 0., 1.) );
   color *= .5*i + .5;
   i = .5*pow( max( 0., abs(dot(rotNorm, dirHalf)) ), 40.);
   color += i;
}
</script>

Vortex decay

Nonlinear wave equation has stationary vortex solutions with the integer winding numbers m of the form
u_m(r) = A_m(r) exp(imθ).
It is known [1] that the m = 1 vortices are stable and m ≥ 2 vortices are unstable. In this GPU based simulation you see m=2 vertex decay. A simple approximation (the dashed curve) is used for the initial m=2 vertex.

[1] "Quantized vortex stability and interaction in the nonlinear wave equation" Weizhu Bao, Rong Zengc, Yanzhi Zhang.

Simulations on GPU
updated 4 Jan 2011