3D Solid State Crystal models

WebGL models

To see these models you need a modern graphical card and a browser with WebGL support (see get.webgl.org).

3D Bravais Lattices

Bravais lattice is a lattice with translation symmetry which consists of equivalent nodes. There are 14 different Bravais lattices in 3D. Only three Bravais lattices with cubic symmetry are shown here. Wigner-Zeitz cell consists of all points nearest to a node and has point symmetry of the corresponding Bravais lattice.
Simple Cubic lattice
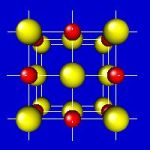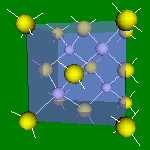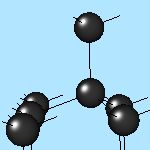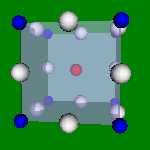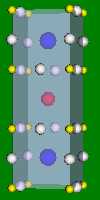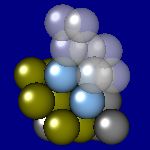
4x4x4 and 6x6x6 cells lattices.
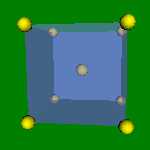
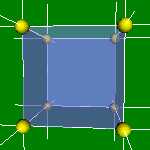
Body Centered Cubic (BCC) unit cell
2x2x2 and 4x4x4 cells lattices. α-Fe, Na, K, β-Ti have this structure. The Wigner-Zeitz cell for the BCC lattice is truncated octahedron.
Face Centered Cubic (FCC) unit cell.
2x2x2 and 4x4x4 lattices. Cu, Au, Ag, Al, Pt, Pd have this structure. The Wigner-Zeitz cell for the FCC lattice is rhombic dodecahedron.

Real crystal lattices

NaCl (KCl, MgO, BaO, CaO, SrO) unit cell.
2x2x2 and 3x3x3 cells. NaCl lattice consists of two FCC sublattices. The Na sublattice is displaced by [1/2,0,0] relative to the Cl sublattice.
GaAs (ZnS, InAs, InP, AlAs, CdTe, HgTe) unit cell.
2x2x2 and 3x3x3 cells. GaAs lattice consists of two FCC sublattices displaced by [1/4,1/4,1/4]
Si (Ge, diamond) unit cell.
2x2x2 and 3x3x3. Diamond lattice is similar to the GaAs one but is made of atoms of one kind.
SrTiO3 (CaTiO3) unit cell. 2x2x2 lattice.
YBa2Cu3O7 is a high temperature superconductive crystal (Tc = 93oK). 2x2x1 lattice.

Crystallographic planes

In crystal with cubic symmetry every [ijk] vector has perpendicular atomic plane (ijk). E.g. parallel to the X axis [100] vector is perpendicular to the (100) atomic plane.
You can easy break NaCl crystall along (100), (010) and (001) equivalent planes. But you cannot break it along (110) plane because you have to destroy more atomic bonds. (111) atomic plane contains charged atoms of one kind and you cannot break crystal along this direction due to electrostatic attraction.
You can break GaAs crystall along (110) plane. Atomic planes (100) and (111) are charged. But you can breake Si along (111) plane because it is uncharged.

Close packed lattices

Close packed Face Centered Cubic unit cell. Close packed hexagonal lattice (Mg, α-Co, α-Be). In close packed lattices you can put the third plane in two different way. FCC and hexagonal lattices are very similar except for FCC includes a close packed plane of the third type.

(100) Si surface reconstruction

Real crystals have broken (unoccupied) bonds on surface which may lead to surface reconstruction. (100) Si surface "before reconstruction". Gray and black balls show two FCC sublattices of Si. 2x1 reconstruction of (100) Si surface.

You can see much more examples at:
"Crystal Structure Tutorials" has a ton of resources on crystal formations that might be useful (thanks to Donna Kennan)
"Materials Science. Introduction to Concepts" by Simon Toh and
Teaching and Education in Crystallography.

E-notes,   WebGL examples     Authors: Evgeny Demidov, Yury Drozdov IPM RAS
updated 22 Oct 2011